a sine wave has an rms amplitude of 2v. what is the peak-to-peak voltage of the wave?
Module 1.ii
Measuring the Sine Moving ridge.
- • Know measurements associated with sine waves
- • a. Meridian to top value.
- • b. Amplitude.
- • c. Height value.
- • d. Periodic time.
- • eastward. Average value.
- • f. RMS value.
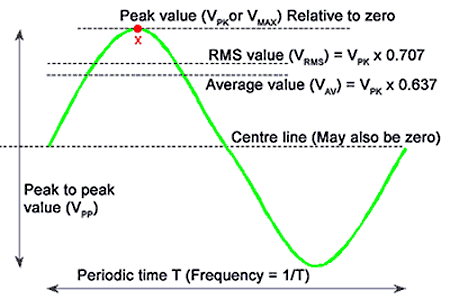
Fig 1.2.1 Characteristics of a Sine Wave
A wave form is a graph showing the variation, usually of voltage or current, against fourth dimension. The horizontal axis shows the passing of time, progressing from left to right. The vertical centrality shows the quantity measured (this is voltage in Fig 1.two.one).
6 of the most important characteristics of a sine wave are;
Height TO Pinnacle value.
INSTANTANEOUS value.
AMPLITUDE.
Tiptop value.
PERIODIC TIME.
Average value.
RMS value.
These characteristics are illustrated in fig 1.two.1
Superlative to Pinnacle Value
The PEAK TO PEAK value is the vertical distance betwixt the top and bottom of the wave. It will exist measured in volts on a voltage waveform, and may be labelled FivePP or 5PK−PK. In a current waveform it would exist labelled IPP or IPK−PK as I (not C) is used to correspond current.
Instantaneous Value
This is the value (voltage or current) of a wave at any particular instant. often called to coincide with another consequence. Due east.k. The instantaneous value of a sine wave 1 quarter of the way through the bicycle will exist equal to the superlative value. Run across bespeak Ten in Fig one.ii.1.
Amplitude
The AMPLITUDE of a sine moving ridge is the maximum vertical distance reached, in either direction from the centre line of the wave. As a sine wave is symmetrical about its centre line, the amplitude of the wave is one-half the height to peak value, equally shown in Fig i.ii.2.
Peak Value
The PEAK value of the wave is the highest value the wave reaches in a higher place a reference value. The reference value commonly used is nil. In a voltage waveform the peak value may exist labelled VPK or FiveMAX (IPK or IMAX in a current waveform).
If the sine moving ridge existence measured is symmetrical either side of zero volts (or zip amperes), meaning that the dc level or dc component of the wave is zero volts, then the peak value must be the aforementioned as the amplitude, that is one-half of the elevation to elevation value.
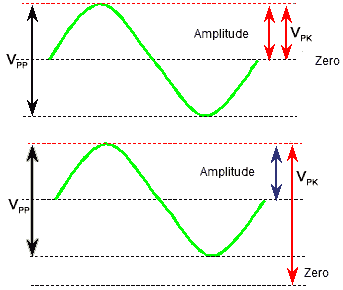
Fig ane.2.ii Defining the Superlative value FivePK
Yet this is not e'er the instance, if a dc component other than zip volts is likewise present, the sine wave will be symmetrical about this level rather than zero. The bottom waveform in Fig one.2.2 shows that the peak value can at present be even larger than the tiptop to peak value, (the aamplitude of the wave however, remains the same, and is the divergence between the acme value and the "heart line" of the waveform).
Periodic Time & Frequency
The PERIODIC Fourth dimension (given the symbol T) is the time, in seconds milliseconds etc. taken for one complete bike of the wave. It can be used to observe the FREQUENCY of the wave ƒ using the formula T =i/ƒ
Thus if the periodic fourth dimension of a wave is 20ms (or one/50th of a second) then in that location must exist l complete cycles of the moving ridge in ane second. A frequency of l Hz. Note that when you use this formula, if the periodic time is in seconds then the frequency will be in Hz.
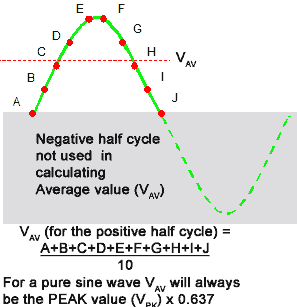
Fig 1.2.iii The Average Value of a Sine Wave
Average Value
The AVERAGE value. This is ordinarily taken to mean the average value of simply one-half a bicycle of the wave. If the average of the total cycle was taken information technology would of class be zero, as in a sine moving ridge symmetrical most zero, in that location are equal excursions above and below the naught line.
Using only one-half a cycle, as illustrated in fig 1.2.iii the average value (voltage or current) is always 0.637 of the peak value of the moving ridge.
VAV = VPK x 0.637
or
IAV = IPK X 0.637
The average value is the value that commonly determines the voltage or current indicated on a examination meter. There are notwithstanding some meters that will read the RMS value, these are chosen "True RMS meters".
The RMS Value.
The RMS or ROOT MEAN SQUARED value is the value of the equivalent direct (non varying) voltage or current which would provide the same free energy to a circuit as the sine wave measured. That is, if an Air conditioning sine wave has a RMS value of 240 volts, it volition provide the same free energy to a circuit as a DC supply of 240 volts.
It can be shown that the RMS value of a sine wave is 0.707 of the meridian value.
FiveRMS = VPK x 0.707 and IRMS = IPK x 0.707
Also, the peak value of a sine wave is equal to 1.414 x the RMS value.
The Form Factor
If VAV (0.637) is multiplied by one.eleven the reply is 0.707, which is the RMS value. This deviation is called the Form Factor of the moving ridge, and the relationship of 1.xi is only true for a perfect sine wave. If the wave is another shape, either the RMS or the average value (or both) volition change, and so will the human relationship between them. This is important when measuring AC voltages with a meter as it is the boilerplate value that near meters really mensurate. Nonetheless they display the RMS value merely by multiplying the voltage by 1.xi. Therefore if the AC moving ridge being measured is not a perfect sine wave the reading will be slightly incorrect. If yous pay enough coin notwithstanding, you lot can buy a true RMS meter that actually calculates the RMS value of not-sine waves.
The Mains (Line) Supply
To demonstrate some of these characteristics in use, consider a very common sine wave, the mains supply or line waveform, which in many parts of the world is a nominal 230V.

Electrical equipment that connects to the mains supply ever carries a label giving information almost what supply the equipment can be continued to. These labels are quite variable in appearance, only often in that location is a picture of a sine wave showing that an a.c. supply must be used. The voltage quoted will be 230V (or 120V in the United states of america)or range of voltages including these values. These voltages really refer to the RMS value of the mains sine moving ridge. The label also states that the frequency of the supply, which is 50Hz in Europe or 60Hz in the USA.
From this minor amount of data other values can be worked out:
a. The tiptop voltage of the waveform, as VPK = VRMS x i.414
b. The AVERAGE value of the waveform, as VAV = VPK x 0.637
c. The Height TO PEAK value of the waveform. This is twice the Aamplitude, which (because the mains waveform is symmetrical about zero volts) is the same value equally VPK.
Because VPK is already known from a. it follows that VPP = FivePK ten 2
d.The PERIODIC Fourth dimension which is given by T =one/ƒ
Source: https://learnabout-electronics.org/ac_theory/ac_waves02.php
0 Response to "a sine wave has an rms amplitude of 2v. what is the peak-to-peak voltage of the wave?"
Post a Comment